In our previous post, we delved into the Jolt zkVM and uncovered several significant bugs in the code. In this post, we will provide a detailed walkthrough on how Jolt actually works.

Jolt is a zero-knowledge Virtual Machine (zkVM) designed for the RISC-V architecture and developed by a16z. It employs the Lasso lookup argument to prove the correctness of VM execution. While often praised as the simplest zkVM, Jolt is a relatively new protocol with limited resources explaining its functionality.

This post is primarily sourced from the Jolt source code, the Jolt book, and the original papers on Lasso and Jolt.

Overview

In Jolt, a program will be compiled into RISC-V binary first. Then, the Jolt RISC-V emulator will run and execute the binary to generate the execution traces. From these execution traces, the prover can generate a proof that can later be verified by the verifier.

The image below, from the Jolt paper, illustrates the overview of how execution traces are being proved.

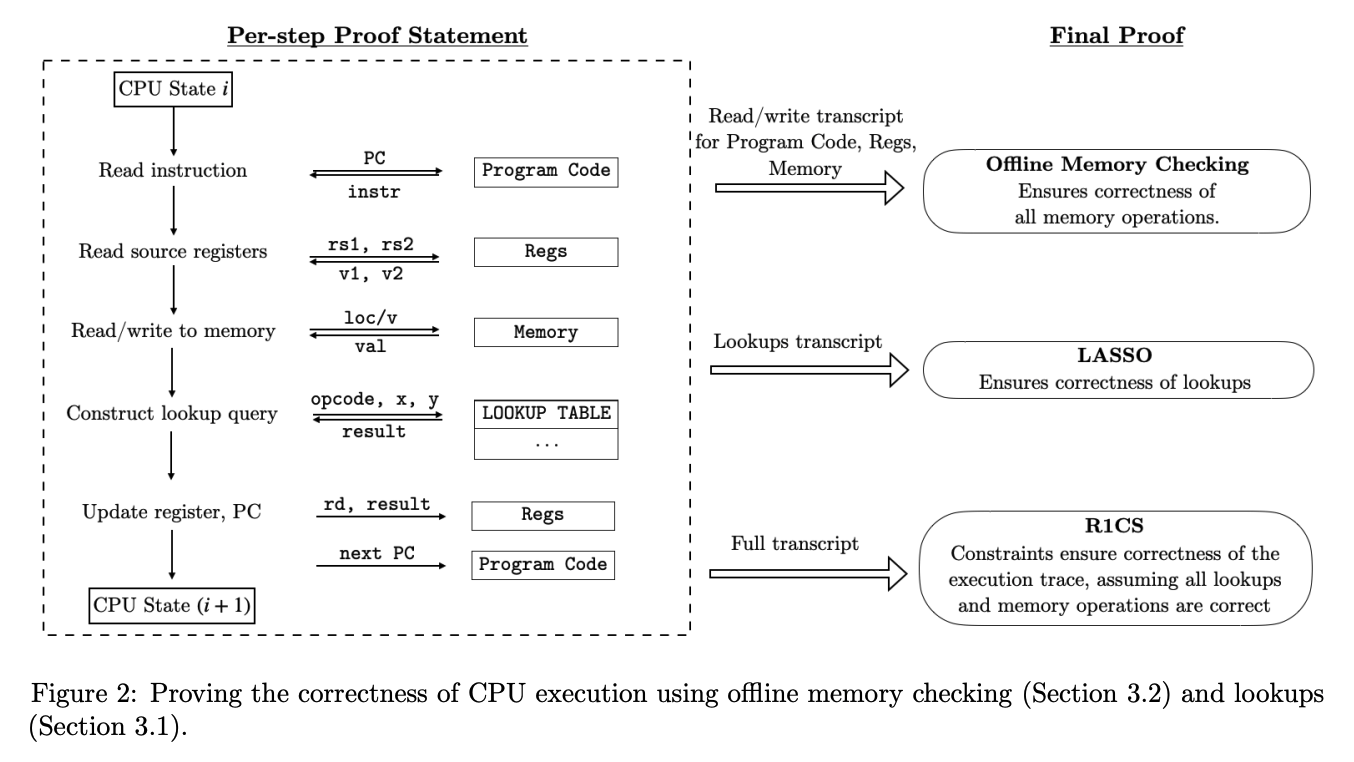
So, according to the image above, there are three main components to prove the correctness of execution traces:

1. Instruction lookup
2. Offline memory checking
3. Rank-1 Constraint System (R1CS)

In the next section, we will explore each of them in detail.

Instruction Lookup

In Jolt, the correctness of the evaluation of VM instructions is proved for the most part using lookup tables, which are linked to the proof systems via a lookup argument.

Essentially, a lookup argument is a cryptographic protocol that allows the prover to demonstrate that a set of values exists within a predefined table, without revealing additional information about the computation. For example, to prove $1+2=3$, we can simply perform a lookup into table $T$ using $1$ and $2$ as index to get the result $3$. This can be done effectively using a lookup argument called Lasso.

Consider a vector $T \in \mathbb{F}^{n}$ as lookup table, and a binary matrix $a \in \mathbb{F}^{s \times n}$ as the corresponding lookup indices where each row only has a single $1$, representing the index of table $T$, with $n$ and $s$ being the size of $T$ and the number of lookups, respectively.

Then, the lookup argument enables a prover to convince a verifier that the vector of values $v$ is contained in the indices $a_i$ of the table $T$, that is $T[a_i] = v_i$ for all $i$.

Naively, to check that $T[a_i] = v_i$, the verifier can simply check the following equality:

$$ a \cdot T = v $$

However, this simple dot product is very unpractical to do in practice as the size of these values is very big. So, we can transform the above equality check into the following sumcheck protocol instance for a random $r$

$$ \displaystyle\sum_{y \in {0, 1}^{\log n} } \widetilde{a}(r,y) \cdot \widetilde{T}(y) = \widetilde{v}(r) $$

where $\widetilde{T}$, $\widetilde{a}$, and $\widetilde{v}$ represent the multilinear extension (MLE) of the respective values.

The sumcheck protocol itself is an interactive proof that verifies the sum of a multivariate polynomial over a Boolean hypercube by recursively reducing the problem to univariate polynomials. The details of the sumcheck protocol and the MLE are outside the scope of this post. We suggested to look at the following resource here to understand how it works.

Continuing our previous expression, we can still optimize it further. Keep in mind that $a$ is sparse where each row contains only one $1$ and $0$ in the other entries, so we can reformulate the left-hand side to only sum over the lookups instead of the table entries:

$$ \displaystyle\sum_{j \in {0, 1}^{\log s} } \widetilde{eq}(j,r) \cdot T[dim(j)] = \widetilde{v}(r) $$

Where $dim(j)$ is the lookup index of row $j$, and $\widetilde{eq}(j,r)$ is the MLE of the function:

$$ eq(j,r) = \begin{cases} 1 & \text{if}\ r=j \newline 0 & \text{otherwise} \end{cases} $$

However, since $T$ is very big ($2^{64}$ rows for 32-bit), it’s unpractical to materialize. We can decompose $T$ into smaller chunks (say 4 bit per chunk for 32-bit, i.e. $c=16$).

$$ \displaystyle\sum_{j \in {0, 1}^{\log s} } \widetilde{eq}(j,r) \cdot g(T_1[dim_1(j)], …, T_c[dim_c(j)]) = \widetilde{v}(r) $$

where $g(x_1, …, x_c)$ is a $c$-variate polynomial that is the multilinear extension of $f(x_1, …, x_c)$, acting as a collation function to “concat” the chunks together. These chunks are called “subtable” in Jolt.

Since $T_i[dim_i(j)]$ must be in the polynomial form, we can reformulate them as follows

$$ \displaystyle\sum_{j \in {0, 1}^{\log s} } \widetilde{eq}(j,r) \cdot g(E_1(j),…,E_c(j)) = \widetilde{v}(r) $$

where $E_i(j)$ are polynomials that represent the $T_i[dim_i(j)]$ committed by the prover.

And that is the final expression that needs to be calculated by sumcheck at a random point $r$ from the verifier. This is called “primary sumcheck” in Jolt.

In the Lasso protocol, the prover provides the commitment $E_i$ to the verifier. However, so far, the verifier cannot guarantee that $E_i$ is actually the values from $T_i$ such that $E_i(j) = T_i[dim_i(j)]$. That’s why we need the second component of Jolt, which is called offline memory checking.

Offline Memory Checking

Offline memory checking is the second component of Jolt. It allows the prover to convince the verifier that read/write operations were performed correctly.

In Jolt, memory checking is used in three different locations:

1. Instruction lookup: ensures $E_i$ in instruction lookup operation are correct
2. Bytecode: ensures that execution traces are part of the actual program bytecode
3. Memory read/write: ensures read/write memory (register, RAM, and program I/O) is correct

Essentially, offline memory checking allows the verifier to ensure that a read operation on a specific memory address returns the most recently written value for that address.

First, let us define four sets $init$, $final$, $read$, and $write$ that represent the initial, final, read, and write memory sets, respectively:

$$ init, final \subseteq {(a_i, v_i, t_i) \vert i \in [0,M]} $$

$$ read, write \subseteq {(a_i, v_i, t_i) \vert i \in [0,m]} $$

Here, $a,v,t$ represent the address, value, and timestamp (counter of memory access), respectively, with $M$ being the size of memory, and $m$ being the total number of memory operations.

Basically, the verifier can check the correctness of memory operation with the following equality check, regardless of the sequence of elements:

$$ read \cup final = write \cup init $$

We can effectively perform the equality check with a multiset hash applied to each set instead of checking the element individually.

So, the check becomes

$$ H_{\gamma,\tau}(read) \cdot H_{\gamma,\tau}(final) = H_{\gamma,\tau}(write) \cdot H_{\gamma,\tau}(init) $$

with the following homomorphic hash function $H$

$$ H_{\gamma,\tau}(S) = \prod_{(a_i,v_i,t_i) \in S} h_{\gamma,\tau}(a_i,v_i,t_i) $$

where $h$ is the Reed-Solomon fingerprint for random $\gamma$ and $\tau$ from the verifier:

$$ h_{\gamma,\tau}(a,v,t) = a \cdot \gamma^2 + v \cdot \gamma + t - \tau $$

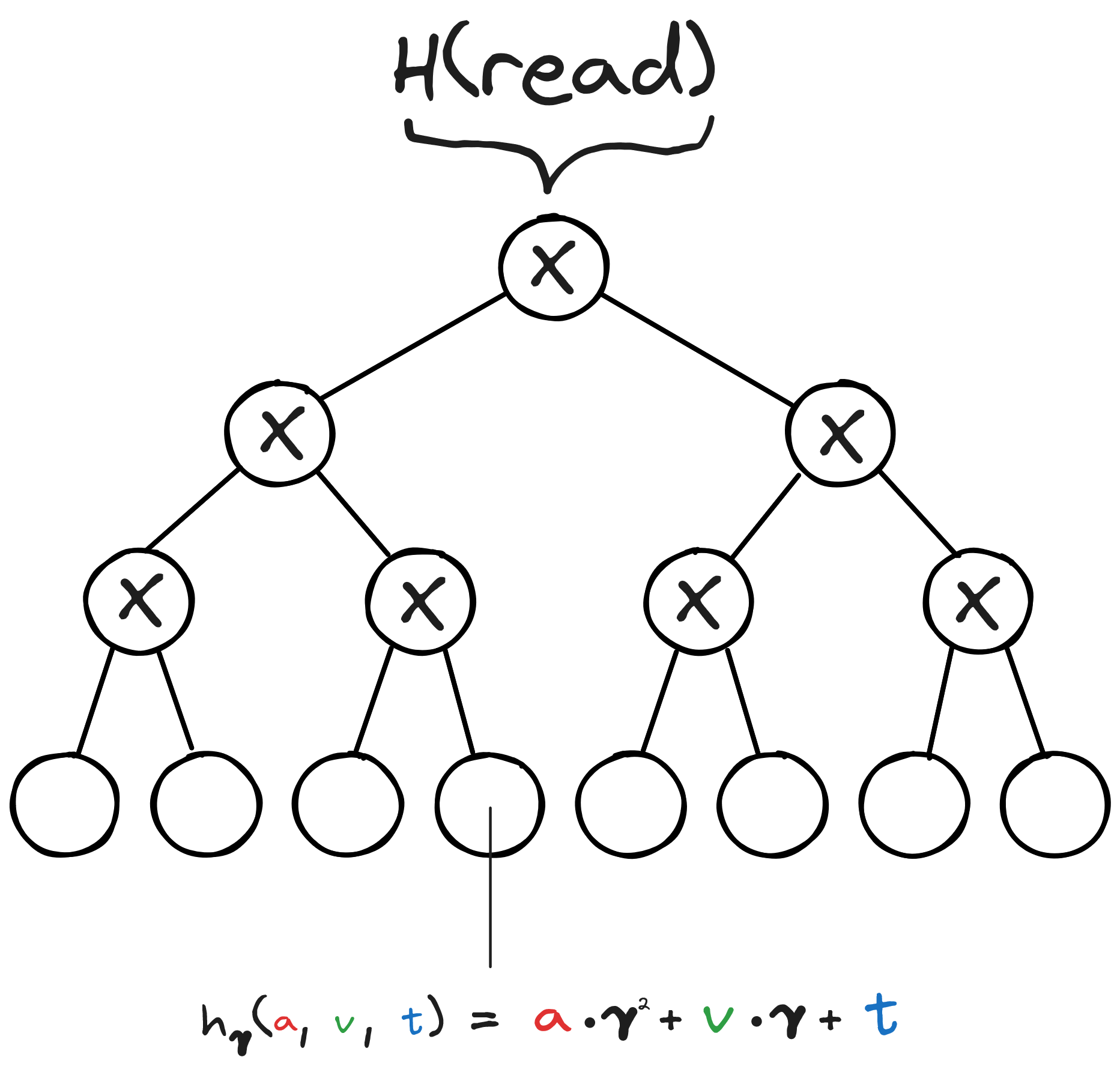
In the Jolt implementation, this multiset hashing $H$ is represented by a binary tree circuit of multiplication gates and computed using an optimized GKR protocol. So, each leaf is the computation result of $h$ for each set element.

Consider the following image from Jolt’s repository to get a clearer picture of how the hash is represented:

Memory Checking In Instruction Lookup

Continuing our previous instruction lookup explanation, to ensure that $E_i(j) = T_i[dim_i(j)]$, we can transform this problem to become memory checking of $T$ being read $\log s$ times. In other words, $E_i(j)$ and $dim_i(j)$ are equivalent to $v_i$ and $a_i$, respectively. The memory checking will ensure that a read operation to the memory address $a_i$ is indeed the value $v_i$.

At first, the verifier can easily construct the $init$ memory set, where $t_i$ is zero for all $i$, and compute the MLE of each leaf with the following:

$$ h_{\gamma,\tau}(init_i) = \left(\displaystyle\sum_{i=1}^{\log M}2^{i-1} \cdot k_i\right) \cdot \gamma^2 + \widetilde{T_i}(k) \cdot \gamma + 0 - \tau $$

For the $read$ and $write$ memory sets, the verifier needs the list of read memory addresses which is represented in $dim_i$ from the prover commitment, along with the value from $E_i$ and the timestamp from $read\text{-}cts_i$ and $read\text{-}cts_i+1$ for $read$ and $write$, respectively.

$$ h_{\gamma,\tau}(read_i) = dim_i(k) \cdot \gamma^2 + E_i(k) \cdot \gamma + read\text{-}cts_i(k) - \tau $$

$$ h_{\gamma,\tau}(write_i) = dim_i(k) \cdot \gamma^2 + E_i(k) \cdot \gamma + read\text{-}cts_i(k) + 1 - \tau $$

The procedure for the $final$ memory set is similar to the one for the $init$ memory set. The main difference is that the timestamp is computed from $final\text{-}cts_i$ representing the total number of lookups which is also committed by the prover.

$$ h_{\gamma,\tau}(final_i) =\left(\displaystyle\sum_{i=1}^{\log M}2^{i-1} \cdot k_i\right) \cdot \gamma^2 + \widetilde{T_i}(k) \cdot \gamma + final\text{-}cts_i(k) - \tau $$

Memory Checking In Bytecode

In Jolt, a single CPU step (eg. add x0, x0, x0) is represented by what is called bytecode. Each bytecode element contains the following values:

• address: Memory address of the instruction in the binary
• bitflags: Packed binary flags that determine the type and property of the instruction and later used in R1CS
• rd: Index of the destination register of the instruction
• rs1: Index of the first source register of the instruction
• rs2: Index of the second source register of the instruction
• imm: Immediate value for the instruction

In order to check if execution traces that were being proved are subset elements of the actual bytecode of the program, we can simply use memory checking to prove the read operation of the table $T$ which is the program bytecode.

However, there is a small difference of the set element used in this process. Instead of $(a,v,t)$, each set element is $(a,v_{bitflags},v_{rd},v_{rs1},v_{rs2},v_{imm},t)$.

So, to compute $h$, the calculation becomes:

$a \cdot \gamma^6 + v_{bitflags} \cdot \gamma^5 + v_{rd} \cdot \gamma^4 + v_{rs1} \cdot \gamma^3 + v_{rs2} \cdot \gamma^2 + v_{imm} \cdot \gamma + t - \tau$

Note that in this part, the prover doesn’t need to provide any commitment since it is assumed that the program bytecode is sufficiently short and the verifier can compute the MLE on its own.

Memory Checking In Read/Write Memory

A zkVM program needs to handle and expose program input and output to the verifier, so that they can be checked to match certain statements.

However, as we’ve seen in the offline memory checking, the verifier doesn’t really have complete knowledge of the memory value. So, how does Jolt handle this?

First, let’s see how the read-write memory structure is mapped in Jolt:

Read-write memory in Jolt is structured as one unified address space that is separated into three main regions which are Registers, Program I/O, and RAM.

Registers is the memory region where all VM registers and virtual registers live. For a 32-bit architecture, this area will be of size $2^6$ (32 VM registers and 32 virtual registers).

Program I/O contains inputs, outputs, panic bit, termination bit, and zero-padding until the size of this area is a power of two. All values in this area are known to verifier.

RAM is the memory region where the stack and the heap live. This area is also padded with zero values until the whole size of the memory is a power of two (which is the max memory size that was set before).

To check the correctness of registers and RAM, we can perform offline memory checking as usual by combining registers and RAM as one set elements. But, for the program I/O, we need to perform an additional check.

Note that the verifier can compute the MLE of $init$ by themselves since the input is known to verifier and the rest is zero. However, they cannot compute the MLE of $final$ since register and RAM are not known to the verifier throughout VM execution.

What the verifier can do is to compute the MLE of the program I/O, namely $io$ to be equal to $final$. This equality check can be performed via the sumcheck protocol to enforce a “zero-check” on the difference of $io$ and $final$:

$$ \displaystyle\sum_{x \in {0,1}^{\log M}} \widetilde{eq}(r, x) \cdot \widetilde{io\text{-}range}(x) \cdot (final - io) \stackrel{?}{=} 0 $$

Where $\widetilde{io\text{-}range}(x)$ is the MLE of the function:

$$ io\text{-}range(x) = \begin{cases} 1 & \text{if}\ io\text{-}start \le x \le ram\text{-}offset \newline 0 & \text{otherwise} \end{cases} $$

$io\text{-}start$ and $ram\text{-}offset$ represent the offset index of program I/O and RAM in the memory, respectively.

But, there is still one last thing that we need to take care of. So far, we’ve dealt with read-only memory checking. But this time, to ensure the correctness of registers and RAM, the previous multiset equality check is not enough, since registers and RAM are writable memory.

In a read-write context, we need one additional check to verify that each read operation must not retrieve a value that was written in the future.

Essentially, the verifier needs to ensure that the timestamp of each read operation, referred to as the read timestamp, is less than or equal to the global timestamp. This global timestamp begins at 0 and increments by one with each step.

This problem is equivalent to checking that the read timestamp and the global timestamp substracted by the read timestamp lie within the range $[0, m)$ where $m$ is the length of the execution trace. So, this is basically a range check which can be done via Lasso by treating this problem as a lookup to the table $[0, 1, …, m-1]$.

In summary, to check the correctness of the read-write memory operation, we need to perform three things:

1. Offline memory checking
2. Handle program I/O via sumcheck
3. Timestamp range check via Lasso

Rank-1 Constraint System (R1CS)

We have handled that instructions are executed correctly and all memory operations are done correctly from the two previous components.

However, we have not handled that:

• Execution traces are in the correct order according to the bytecode address and the program counter PC (including jump and branch)
• Instruction lookups are using the correct lookup indices from actual operands (whether it is rs1, rs2, and/or imm)
• Instruction lookup inputs and outputs are consistent with the value read/written from/to memory

To handle those problems, here comes the last component of Jolt to ensure that the whole VM process (fetch-decode-execute) is correct by gluing and constraining the steps involved via an R1CS.

The complete constraints in Jolt can be seen in the constraints.rs.

Note that most of the R1CS constraints in Jolt are uniform, such that the constraint matrices for the entire program are identical replicas of the constraint for a single VM instruction. The only non-uniform constraint is the constraint that checks the transition of PC to the next step.

R1CS Inputs & Bitflags

Given matrices $A,B,C \in \mathbb{F}^{m \times m}$, the satisfiability of an R1CS is true if and only if

$$ (A \cdot z) \circ (B \cdot z) - (C \cdot z) = 0 $$

where $A,B,C$ are the constraints and $z$ is the witness of the R1CS. This is what the prover needs to prove that they know such $z$. So, each constraint must be of the form of $a \cdot b - c = 0$.

In order to construct those, Jolt uses inputs from the execution traces, where each trace (single CPU step) contains the bytecode element, instruction lookup, and read-write memory operation.

Jolt also uses bitflags from the bytecode as R1CS input to “toggle” certain constraints. For example, if we want to check the equality of $x$ and $y$ only if $flag$ is true, then the R1CS constraint is as follows:

$$ flag \cdot (x - y) = 0 $$

Bitflags is a 64-bit length binary that contains two separate flags concatenated together, which are called circuit flags and instruction flags.

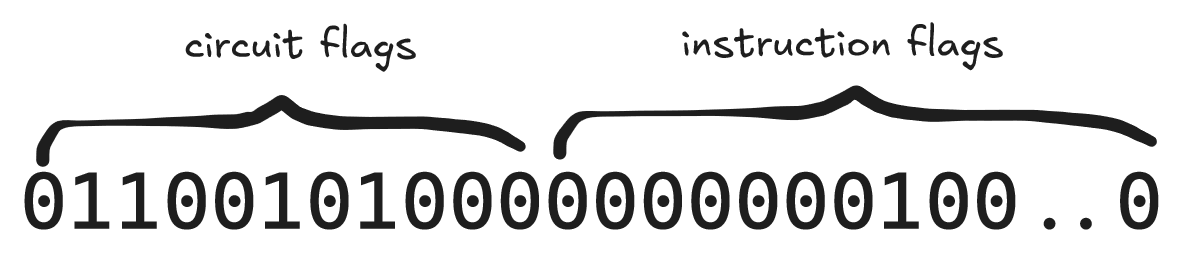
Circuit flags is multiple flags that can be set to match a certain property of the instruction. The following is a complete list of circuit flags implemented in Jolt:

1. Is the first lookup operand PC?
2. Is the second lookup operand imm?
3. Is this a load instruction?
4. Is this a store instruction?
5. Is this a jump instruction?
6. Is this a branch instruction?
7. Does this instruction update rd?
8. Does this instruction involve concatenation on the lookup?
9. Is this a virtual instruction?
10. Is this an assert instruction?
11. Does this instruction require to not update the program counter PC?

Note that above list is taken from the current Jolt code (at the time of writing) which is slightly deviated from those described in Appendix A.1 of the Jolt paper.

Meanwhile, instruction flags is a single flag (one-hot vector) that determines what type of instruction is executed (is it addition, subtraction, multiplication?). Thus, the ADD and ADDI instructions, for example, will use the same instruction flag.

As an example, let’s say we want to build a constraint to ensure that the value written to rd is equal to the instruction lookup output.

Let’s define $\text{rd_bytecode}$ as the value of rd in the program bytecode and $\text{flag}_{7}$ as the value of the 7th circuit flags. First, we set an auxiliary variable $\text{condition}$:

$$ \text{condition} \leftarrow \text{rd_bytecode} \cdot \text{flag}_{7} $$

This variable should be non-zero if both $\text{rd_bytecode}$ and $\text{flag}_{7}$ are also non-zero.

Note that we need to add the constraint such that $\text{condition}$ is actually equal to $\text{rd_bytecode} \cdot \text{flag}_{7}$. Otherwise, this would become underconstrained bug:

$$ \text{rd_bytecode} \cdot \text{flag}_{7} - \text{condition} = 0 $$

Then, the main constraint is as follows:

$$ \text{condition} \cdot (\text{rd_write} - \text{lookup_output}) = 0 $$

Here, $\text{rd_write}$ is the value written to rd from the read-write memory operation and $\text{lookup_output}$ is the result of the instruction lookup. This constraint ensures that $\text{rd_write}$ must be equal to $\text{lookup_output}$.

R1CS Satisfiability

After the R1CS constraints and witness are constructed, Jolt uses Spartan to prove the satisfiability of the R1CS from the given witness.

The details of how Spartan works are outside the scope of this post. In short, Spartan essentially transforms an R1CS instance into sumcheck instances which can be efficiently proved by using two sumcheck protocols. It also requires a multilinear polynomial commitment scheme (eg. Hyrax, HyperKZG, etc.) to commit to the evaluation of the given witness.

Putting It All Together

Let’s combine all the Jolt components and summarize how the full protocol is carried out.

Note that in practice, we use a non-interactive version where all verifier random challenges are generated from a Fiat-Shamir heuristic.

Setup

In the setup phase, both prover and verifier agree on the following:

1. Polynomial commitment scheme that will be used throughout the protocol (this includes Structured Reference String (SRS) and curve that is used for the relevant PCS)
2. Bytecode of the provable program
3. Chunk size to decompose table lookup
4. Max memory size

Then, both prover and verifier can construct lookup subtables and memory layouts based on the agreed upon chunk size and max memory size, respectively.

Proving

The prover runs the provable program with some given inputs, and then generates the execution traces and program I/O.

From the generated execution traces and program I/O, the prover performs the following in order:

1. Pad the execution traces until the trace length is a power of two, filled with NOP instruction.
2. Prove that bytecode in the execution traces is part of bytecode in the setup phase with offline memory checking.
3. Prove that all instruction lookups in the execution traces are correct with primary sumcheck and offline memory checking.
4. Prove that all read-write memory operations in the execution traces are correct with offline memory checking.
5. Prove that program I/O is valid with sumcheck protocol.
6. Prove that read timestamps in memory operations are correct with timestamp range check.
7. Prove the correctness of the R1CS with Spartan.
8. Prove all opening commitments that are used over the course of the protocol.
9. Send all the proofs along with the commitments and the program I/O to the verifier.

Verifying

From the given proofs, commitments, and program I/O from the prover, the verifier performs the following:

1. Verify bytecode memory checking proof
2. Verify instruction lookup from the primary sumcheck and memory checking proof
3. Verify read-write memory proof
4. Verify program I/O sumcheck proof
5. Verify timestamp range check proof
6. Verify Spartan proof
7. Verify all opening proofs of the commitments

If all these checks pass, the verifier can safely assume that the given program I/O is valid. Then, the verifier can check if the given program I/O match certain statement.

Conclusion

This post explored how Jolt proves and verifies the correctness of VM execution. The use of the Lasso lookup argument makes Jolt a very simple and extensible zkVM, as we can easily add more VM instructions by simply updating the lookup table used in the instruction lookup.

Jolt is actively maintained and constantly improving with many optimizations and exciting features which you can explore in the official repository.